Nasz zespół prawników i analityków specjalizuje się w rozliczeniach oraz analizie matematycznej / finansowej umów kredytowych.
W szczególności wykonujemy opinie rachunkowe, których celem jest ustalenie prawidłowości rozliczenia umowy kredytu indeksowanego CHF (oraz innymi walutami) - zgodnie z obowiązującymi normami kodeksowymi, zasadami matematyki finansowej, zapisami umowy kredytu oraz aktualnym orzecznictwem.
Nasze opinie rachunkowe w zakresie kredytów indeksowanych CHF zawierają wyliczenia:
-
Stopy procentowej zastosowanej w umowie leasingu
-
Marży finansującego
-
Dyskonta
-
Kapitału pozostałego do spłaty
-
Opłat zaległych
-
Opłat dodatkowych
-
Kwoty do zapłaty / zwrotu z tytułu zakończenia umowy przed czasem
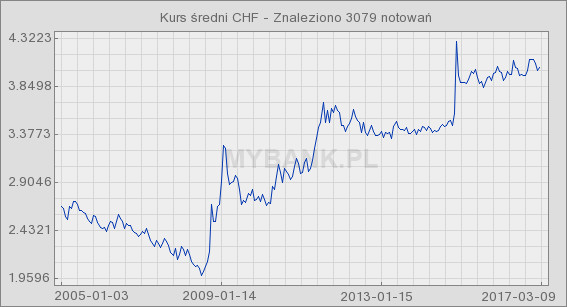Wykres kursów CHF wygenerowany za pomoca portalu mybank.pl na postawie kursów średnich NBP
W naszych analizach umów kredytowych wykorzystujemy:
- macierze przepływów finansowych do płatności w walucie oraz po indeksie (raty przeliczane po kursie aktualnym banku, kursie średnim NBP, kursie banku z dnia podpisania umowy kredytu)
- funkcję matematyki finansowej Ms Excel „Rate”
- funkcję matematyki finansowej Ms Excel „IRR” dla harmonogramu umowy leasingowej, uwzględniając przepływy finansowe (wpłaty i wypłaty)
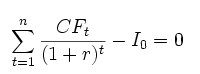
gdzie:
CFt – przepływy gotówkowe w okresie t,
r – stopa procentowa,
Io – nakłady początkowe,
t – kolejne okresy
- funkcję matematyki finansowej Ms Excel „PV”
- funkcję matematyki finansowej Ms Excel „NPV”
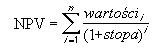
Obliczenia przeprowadzamy również manualnie z wykorzystaniem wzorów matematyki finansowej.
W metodzie annuitetowej mamy ciąg rosnący dla rat kapitałowych:
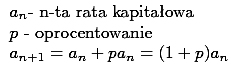
Zatem w przypadku harmonogramów z ratami równymi w umowach leasingu, mamy ciąg rosnących rat kapitałowych oraz malejące części odsetkowe rat.
Wartość raty w schemacie rat równych jest wyznaczana ze wzoru:
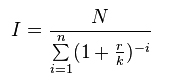
gdzie:
I – wysokość raty równej,
N – kwota udzielonego "kredytu rzeczowego",
r – oprocentowanie kredytu w skali roku,
k – liczba rat płatnych w ciągu roku (np. k = 4 dla rat płatnych co kwartał),
n – liczba rat.
W schemacie spłat w ratach równych płatności kapitałowe w kolejnych okresach tworzą ciąg geometryczny.
Inny powszechnie stosowany wzór na ratę w annuicie:
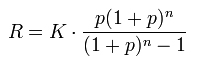
gdzie:
R - rata kredytu,
K - kwota kredytu,
p - stopa procentowa kredytu dla jednego okresu n,
n - liczba rat.
Wykonujemy dyskontowanie za pomocą współczynników dyskontujących.
Dyskonto w umowie kredytowej
Dyskonto – wartość, o jaką należy pomniejszyć przyszłą wartość, aby otrzymać bieżącą wartość. Dyskontowanie jest działaniem odwrotnym do oprocentowania.
Współczynnik dyskontowy
Współczynnik dyskontowy – wartość bieżąca jednostki monetarnej, o określonym terminie płatności w przyszłości. Stanowi czynnik, który zrównuje wartość przyszłą kapitału z jego wartością bieżącą. Różnica pomiędzy wartością przyszłą a wartością bieżącą kapitału wynika ze zmienności wartości pieniądza w czasie. Współczynnik dyskontowy dany jest wzorem:
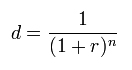
gdzie:
d - współczynnik dyskontowy
r - stopa procentowa
n - liczba okresów
Dokonujemy wizualizacji spłaty umowy leasingu oraz "kredytu rzeczowego"
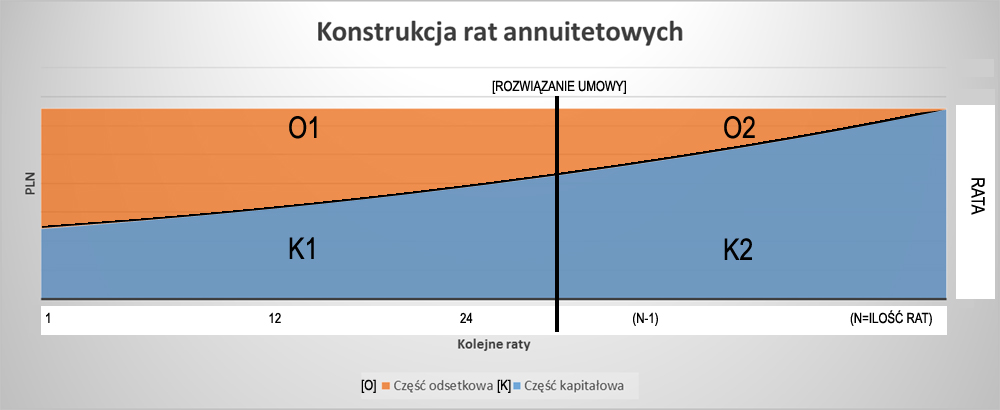
Powyższy wykres prezentuje graficzny przebieg spłaty zobowiązania przy harmonogramie rat równych.
ODSETKI CAŁKOWITE = O = O1 +O2
ODSETKI NALICZONE PRZED ROZWIĄZANIEM UMOWY NALEŻNE BANKOWI = O1
ODSETKI PO ROZWIĄZANIU UMOWY NIE NALEŻNE BANKOWI [korzyść w rozumieniu normy art. 70915 k.c.] = O2
KAPITAŁ CAŁKOWITY = K = K1 + K2
KAPITAŁ NALICZONY PRZED ROZWIĄZANIEM UMOWY = K1
KAPITAŁ WYMAGALNY PO ROZWIĄZANIU UMOWY = K2
Zgodnie z przyjętymi zasadami, po rozwiązaniu umowy kredytu, bank może żądać wyłącznie przyszłych rat kapitałowych. Na wykresie wartość kapitału pozostałego do spłaty oznaczona została sygnaturą [K2].
Żądanie przez bank odszkodowania przekraczającego wartość [K2] prowadzi do bezpodstawnego wzbogacenia (wadliwe dyskontowanie). Z chwilą rozwiązania umowy odpadł obowiązek kredytowania kredytobiorcy.
Ustawa o Kredycie Konsumenckim
Poniżej prezentujemy kluczowe przepisy ustawy o kredycie konsumenckim w zakresie poprawności rozliczenia:
Art. 5. Pkt 6 Całkowity koszt kredytu – wszelkie koszty, które konsument jest zobowiązany ponieść w związku z umową o kredyt, w szczególności:
a) odsetki, opłaty, prowizje, podatki i marże jeżeli są znane kredytodawcy oraz
b) koszty usług dodatkowych w przypadku gdy ich poniesienie jest niezbędne do uzyskania kredytu
– z wyjątkiem kosztów opłat notarialnych ponoszonych przez konsumenta;
Art. 48. Konsument ma prawo w każdym czasie do spłaty całości lub części kredytu przed terminem określonym w umowie.
Art. 49 ust. 1. W przypadku spłaty całości kredytu przed terminem określonym w umowie, całkowity koszt kredytu ulega obniżeniu o te koszty, które dotyczą okresu, o który skrócono czas obowiązywania umowy, chociażby konsument poniósł je przed tą spłatą.
2. W przypadku spłaty części kredytu przed terminem określonym w umowie, ust. 1 stosuje się odpowiednio.
"W przypadku wcześniejszej spłaty kredytu konsumenckiego kredytodawca powinien proporcjonalnie obniżyć i zwrócić część kosztów takiego kredytu" - to wspólna interpretacja przepisów ustawy o kredycie konsumenckim Rzecznika Finansowego i Prezesa Urzędu Ochrony Konkurencji i Konsumentów z maja 2016 roku.
Wspólne stanowisko Prezesa UOKiK i Rzecznika Finansowego dostępne jest do pobrania ze strony http://www.uokik.gov.pl